Creencias en la geometría

Creencias… ¡Cómo las temo! Las creencias nos colocan sus gafas oscuras en la mente y nos impiden ver con claridad. Cuando una persona tiene una determinada creencia le es imposible escuchar más allá de ella. Esta creencia le susurra en el oído con voz arrulladora, para adormecer su entendimiento. Pero, bueno, de lo que yo quería hablar aquí es de las “creencias” en las Matemáticas (que no sobre las Matemáticas) y, concretamente, de esas ideas erróneas relacionadas con aspectos geométricos, que se van pegando como una lapa en la cabeza y que se van transmitiendo de generación en generación en nuestras escuelas.

Para empezar, ¿tienes claro lo que es un rectángulo? Mira las figuras de abajo y piensa cuáles entran dentro de esta clasificación.

Me imagino que no habrás tenido demasiado problema en darte cuenta de que todos esos polígonos son rectángulos… ¿o sí? Quizás te hayan surgido dudas con el último: ¿un cuadrado es un rectángulo? Piensa, piensa… un rectángulo es un paralelogramo (polígono de 4 lados, con los lados paralelos dos a dos) cuyos lados forman ángulos de 90 grados: ¿estás de acuerdo? Y ahora, ¿cumple el cuadrado esas propiedades? Creo que es evidente que sí. Cumple más propiedades, pero esas también.

Sigamos con los cuadriláteros. ¿Son todos los polígonos de la figura rombos?

Veo que esta vez has estado más atento/a. Todos son rombos: los cuadrados también, ya que son paralelogramos con los 4 lados de la misma longitud.

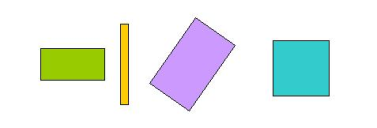
Hay determinados polígonos que nos parecen extraños, como si no encajaran dentro de la clasificación que se les ha querido “encasquetar”. Quizás podríamos llamarlos los “parias” o “rebeldes” de los polígonos: aquellos que parecen no cumplir con las normas, que van a su aire, los discretos, los que “pasan” de seguir la corriente y sobre todo, los que nunca (o casi nunca) tienen un espacio (bidimensional, je, je) en las aulas:

Por ejemplo, el primero de ellos no parece un cuadrilátero (posiblemente, no sé la razón, tenga “más pinta” de triángulo), pero evidentemente lo es. Con el resto ocurre algo parecido. Me pregunto, ¿por qué no se hace más uso de estos polígonos (cóncavos) en las clases? A mí me parecen muy interesantes. Pero bueno, me imagino que es como en nuestra sociedad: hay unos cánones de belleza con los que constantemente somos bombardeados. La “fealdad” no tiene cabida en la televisión, el cine… Los polígonos “feos” tampoco la tienen dentro de las aulas, a pesar de lo mucho que nos podrían enseñar.

Vayamos ahora al concepto de diagonal de un polígono. ¿Cómo la podríamos definir? ¿Te parece bien “segmento (recto) que une vértices del polígono no consecutivos”? Pues bien, a los niños quizás les cueste “ver” que el segmento en rojo de la figura es una diagonal. Parece salirse (y nunca mejor dicho) de lo establecido y, como en la vida misma, esto no es muy bien visto y crea un conflicto.

Muchas veces sólo miramos en una dirección, tenemos una opinión formada sobre las cosas de la que nos es muy difícil desconectar, sin embargo, ¿no es más interesante poder apreciar los distintos aspectos desde múltiples puntos de vista? Si te pido que me dibujes el desarrollo plano de un cilindro, probablemente tu dibujo se asemeje a este:

Mas, ¿por qué quedarnos ahí?, ¿ese es el único desarrollo plano? Mira la siguiente imagen, por poner un ejemplo:

También es un desarrollo plano del cilindro, ¿no? Pues aunque no te lo creas es muy corriente en nuestro mundo. Coge por ejemplo un rollo de papel higiénico. Desecha el papel y quédate con el cartón cilíndrico: intenta deshacerlo con cuidado. Ahí tienes un romboide. ¿Por qué un romboide y no un rectángulo? Porque el romboide proporciona mayor rigidez, ya que la unión es mucho más larga.

Como conclusión y moraleja: no dejemos engañarnos por lo establecido. Hay mucho más de lo que vemos. No encasillemos, o si lo hacemos, estemos dispuestos a rectificar. Que siempre nos hayan mostrado las cosas de una manera no quiere decir que sean así. Las apariencias engañan: lo que en un principio puede parecer un triángulo se convierte en un cuadrilátero si lo vemos más detenidamente. Con las personas y con la vida ocurre lo mismo.

En la escuela se nos presenta esto:

Y yo digo, demos libertad a la imaginación y a la visión de nuestros alumnos y presentémosles esto: